Done with correction, continuing with filling, yum!
This commit is contained in:
parent
1093954710
commit
481dc5eb86
3 changed files with 187 additions and 63 deletions
242
content.tex
242
content.tex
|
|
@ -253,9 +253,9 @@ Par exemple, est-il possible d'avoir des mélodies caractéristiques de l'état
|
|||
\subref{fig:desordonnee}, \subref{fig:part-des} et \subref{fig:reguliere} de la
|
||||
figure \ref{fig:mousses-space}, permettant de les distinguer ?
|
||||
\item{Peut-on écouter les épisodes catastrophiques lors de l'évolution
|
||||
emporelle du système ?} Par exemple, est-il possible d'avoir des mélodies ayant
|
||||
des variations fortes correspondantes aux épisodes catastrophique, les mettant
|
||||
en évidence ?
|
||||
temporelle du système ?} Par exemple, est-il possible d'avoir des mélodies
|
||||
ayant des variations fortes correspondantes aux épisodes catastrophiques, les
|
||||
mettant en évidence ?
|
||||
\end{enumerate}
|
||||
|
||||
Ces deux questions ont orienté notre exploration lors de la
|
||||
|
|
@ -263,13 +263,13 @@ sonification/musification du système. La première est illustrée par les trois
|
|||
états de la figure \ref{fig:mousses-space} ; la seconde est illustrée par les
|
||||
états en fonction du temps de la figure \ref{fig:mousses-time} et le graphe de
|
||||
l'évolution temporelle d'un paramètre de la figure \ref{fig:mousses-graph}.
|
||||
Dans ce graphe, on peut noter trois moment important~:
|
||||
Dans ce graphe, on peut noter trois moments importants~:
|
||||
\begin{enumerate}
|
||||
\item une phase initiale : le système semble statique du point de vue du
|
||||
paramêtre représenté ;
|
||||
\item une phase catastrophique : on trouve plusieurs marches à chaque
|
||||
épisode catastrophique et ils sont difficiles à trouver quand on ne connaît
|
||||
pas le \emph{bon} paramêtre ;
|
||||
paramètre représenté ;
|
||||
\item une phase intermédiaire : on trouve plusieurs marches à chaque épisode
|
||||
catastrophique et ils sont difficiles à trouver quand on ne connaît pas le
|
||||
\emph{bon} paramètre ;
|
||||
\item une phase dite de « scaling state » : le système continue à évoluer mais
|
||||
de manière similaire dans le temps (on ne peut plus distinguer deux images
|
||||
prises à des moments différents de deux dont la seconde est un agrandissement
|
||||
|
|
@ -364,11 +364,11 @@ en nous fondant sur la set-theory.
|
|||
\label{subsec:music}
|
||||
Nous resterons très général sur cette théorie musicale. La notion importante
|
||||
utilisée tout au long de ce mémoire est celle d'\emph{intervalle} : c'est la
|
||||
\emph{hauteur} entre deux notes. Le plus petit intervalle considéré est le
|
||||
demi-ton. Il y a 12 demi-tons dans la gamme occidentale et ils sont répartis
|
||||
sur 7 notes (figure~\ref{fig:gamme}). On peut altérer la hauteur d'une note,
|
||||
donc l'intervalle ayant pour une de ses bornes cette note, en la faisant
|
||||
précéder d'une altération : ♯ (dièse, +1 demi-ton) ou ♭ (bémol, -1 demi-ton).
|
||||
hauteur entre deux notes. Le plus petit intervalle considéré est le demi-ton.
|
||||
Il y a 12 demi-tons dans la gamme occidentale et ils sont répartis sur 7 notes
|
||||
(figure~\ref{fig:gamme}). On peut altérer la hauteur d'une note, donc
|
||||
l'intervalle ayant pour une de ses bornes cette note, en la faisant précéder
|
||||
d'une altération : ♯ (dièse, +1 demi-ton) ou ♭ (bémol, -1 demi-ton).
|
||||
|
||||
\begin{figure}[p]
|
||||
\centering
|
||||
|
|
@ -442,8 +442,9 @@ qui constituent une première formalisation algébrique.
|
|||
\caption{Intervalles et opérations algébriques sur un cercle}
|
||||
\end{figure}
|
||||
|
||||
\bigskip
|
||||
Une autre représentation qui nous intéresse est l'organisation spatiale des
|
||||
intervalles au sein d'un \emph{tonnetz} (figure~\ref{fig:tonnetz}), décrit en
|
||||
intervalles au sein d'un \emph{tonnetz} (figure~\ref{fig:tonnetz}), décrite en
|
||||
premier par Leonhard Euler. Ce dernier a choisi une disposition spatiale
|
||||
compacte valorisant les intervalles\footnote{% (((-----------------------------
|
||||
L. Euler utilise une notation allemande où le $H$ correspond au $B$ anglo-saxon
|
||||
|
|
@ -453,8 +454,8 @@ pour de plus amples détails.}% )))---------------------------------------------
|
|||
~de tierce majeure (4 demi-tons, en progressant sur l'axe horizontal vers la
|
||||
droite) et de quinte juste (7 demi-tons, en progressant sur l'axe vertical vers
|
||||
le bas). Cette représentation est équivalente à la donnée d'un groupe cyclique
|
||||
d'ordre 12 (comme précédemment) mais exprimé sous forme d'un graphe planaire.
|
||||
Ces deux intervalles sont les plus consonnants (après l'octave) ; il est donc
|
||||
d'ordre 12, comme précédemment, mais exprimée sous forme d'un graphe planaire.
|
||||
Ces deux intervalles sont les plus consonnants après l'octave ; il est donc
|
||||
agréable et pratique de pouvoir passer d'une note à une autre en les
|
||||
privilégiants.
|
||||
|
||||
|
|
@ -464,26 +465,27 @@ privilégiants.
|
|||
\subfloat[Tonnetz de L. Euler (1739)]{
|
||||
\includegraphics[width=.45\textwidth]{img/eulers-tonnetz}
|
||||
\label{fig:tonnetz}}
|
||||
\subfloat[Tonnetz de L. Euler vu comme une partie du graphe de Cayley du groupe
|
||||
$\mathbb{Z}_{12}$ avec pour partie génératrice $\{4,7\}$]{
|
||||
\subfloat[Tonnetz de L. Euler vu comme une partie du graphe de Cayley de la
|
||||
présentation finie $<~4,~7;~3\cdot4~=~0,~12\cdot7~=~0~>$ du groupe
|
||||
$\mathbb{Z}_{12}$]{
|
||||
\begin{tikzpicture}
|
||||
[note/.style={draw,black,circle,inner sep=2mm},
|
||||
[note/.style={draw,black,circle,inner sep=.5mm,minimum size=8mm},
|
||||
label distance=-1mm,label position=below left,
|
||||
double distance=.5mm]
|
||||
\node[note,double] (C) [label=Do ] {};
|
||||
\node[note,left=of C] (F) [label=Fa ] {};
|
||||
\node[note,right=of C] (G) [label=Sol ] {};
|
||||
\node[note,right=of G] (D) [label=Ré ] {};
|
||||
\node[note,double] (C) {Do };
|
||||
\node[note,left=of C] (F) {Fa };
|
||||
\node[note,right=of C] (G) {Sol };
|
||||
\node[note,right=of G] (D) {Ré };
|
||||
|
||||
\node[note,above=of F] (A) [label=La ] {};
|
||||
\node[note,right=of A] (E) [label=Mi ] {};
|
||||
\node[note,right=of E] (B) [label=Si ] {};
|
||||
\node[note,right=of B] (Fd) [label= Fa♯] {};
|
||||
\node[note,above=of F] (A) {La };
|
||||
\node[note,right=of A] (E) {Mi };
|
||||
\node[note,right=of E] (B) {Si };
|
||||
\node[note,right=of B] (Fd) { Fa♯};
|
||||
|
||||
\node[note,above=of A] (Cd) [label= Do♯] {};
|
||||
\node[note,right=of Cd] (Gd) [label=Sol♯] {};
|
||||
\node[note,right=of Gd] (Dd) [label= Ré♯] {};
|
||||
\node[note,right=of Dd] (Ad) [label= La♯] {};
|
||||
\node[note,above=of A] (Cd) { Do♯};
|
||||
\node[note,right=of Cd] (Gd) {Sol♯};
|
||||
\node[note,right=of Gd] (Dd) { Ré♯};
|
||||
\node[note,right=of Dd] (Ad) { La♯};
|
||||
|
||||
\draw (F) -- (C) -- node[above,midway] {+7} (G) -- (D);
|
||||
\draw (A) -- (E) -- (B) -- (Fd);
|
||||
|
|
@ -528,24 +530,26 @@ respectivement, comme on peut le voir sur la figure~\ref{fig:trig}.
|
|||
|
||||
\begin{figure}[p]
|
||||
\centering
|
||||
\subfloat[Triangulation d'accords sur un graphe de Cayley, en exemple Do Majeur
|
||||
(gris clair) et La mineur (gris foncé)]{
|
||||
\begin{tikzpicture}
|
||||
[note/.style={draw,black,circle,inner sep=2mm},
|
||||
label distance=-1mm,label position=below left,
|
||||
double distance=.5mm]
|
||||
\node[note,double] (C) [label=Do ] {};
|
||||
\node[note,left=of C] (F) [label=Fa ] {};
|
||||
\node[note,right=of C] (G) [label=Sol ] {};
|
||||
\node[note,right=of G] (D) [label=Ré ] {};
|
||||
[note/.style={draw,black,circle,inner sep=.5mm,minimum size=8mm},
|
||||
label distance=-1mm,label position=above right,
|
||||
double distance=.5mm,scale=.30\textwidth/7.2cm]
|
||||
\node[note] (F) at (0cm,0cm) {Fa };
|
||||
\node[note,double] (C) at (2cm,0cm) {Do };
|
||||
\node[note] (G) at (4cm,0cm) {Sol };
|
||||
\node[note] (D) at (6cm,0cm) {Ré };
|
||||
|
||||
\node[note,above=of F] (A) [label=La ] {};
|
||||
\node[note,right=of A] (E) [label=Mi ] {};
|
||||
\node[note,right=of E] (B) [label=Si ] {};
|
||||
\node[note,right=of B] (Fd) [label= Fa♯] {};
|
||||
\node[note] (A) at (0cm,2cm) {La };
|
||||
\node[note] (E) at (2cm,2cm) {Mi };
|
||||
\node[note] (B) at (4cm,2cm) {Si };
|
||||
\node[note] (Fd) at (6cm,2cm) { Fa♯};
|
||||
|
||||
\node[note,above=of A] (Cd) [label= Do♯] {};
|
||||
\node[note,right=of Cd] (Gd) [label=Sol♯] {};
|
||||
\node[note,right=of Gd] (Dd) [label= Ré♯] {};
|
||||
\node[note,right=of Dd] (Ad) [label= La♯] {};
|
||||
\node[note] (Cd) at (0cm,4cm) { Do♯};
|
||||
\node[note] (Gd) at (2cm,4cm) {Sol♯};
|
||||
\node[note] (Dd) at (4cm,4cm) { Ré♯};
|
||||
\node[note] (Ad) at (6cm,4cm) { La♯};
|
||||
|
||||
\draw (F) -- (C) -- (G) -- (D);
|
||||
\draw (A) -- (E) -- (B) -- (Fd);
|
||||
|
|
@ -581,10 +585,96 @@ double distance=.5mm]
|
|||
\draw[dashed] (Fd.east) -- +(6mm ,0cm );
|
||||
\draw[dashed] (D.east) -- +(6mm ,0cm );
|
||||
\end{tikzpicture}
|
||||
\label{fig:trig}}
|
||||
\quad
|
||||
\subfloat[Dual du graphe de Cayley mettant en exergue une structure
|
||||
hexagonale]{
|
||||
\begin{tikzpicture}
|
||||
[note/.style={draw,black,circle,inner sep=2mm},
|
||||
hex/.style={},
|
||||
label distance=-1mm,label position=below left,
|
||||
double distance=.5mm,scale=.50\textwidth/9.2cm]
|
||||
\begin{scope}[opacity=.5]
|
||||
\node[note] (F) at (-1cm,0cm) {};
|
||||
\node[note,double] (C) at ( 1cm,0cm) {};
|
||||
\node[note] (G) at ( 3cm,0cm) {};
|
||||
\node[note] (D) at ( 5cm,0cm) {};
|
||||
|
||||
\caption{Triangulation d'accords sur un graphe de Cayley, en exemple Do Majeur
|
||||
(gris clair) et La mineur (gris foncé)}
|
||||
\label{fig:trig}
|
||||
\node[note] (A) at ( 0cm,2cm) {};
|
||||
\node[note] (E) at ( 2cm,2cm) {};
|
||||
\node[note] (B) at ( 4cm,2cm) {};
|
||||
\node[note] (Fd) at ( 6cm,2cm) {};
|
||||
|
||||
\node[note] (Cd) at ( 1cm,4cm) {};
|
||||
\node[note] (Gd) at ( 3cm,4cm) {};
|
||||
\node[note] (Dd) at ( 5cm,4cm) {};
|
||||
\node[note] (Ad) at ( 7cm,4cm) {};
|
||||
|
||||
\draw (F) -- (C) -- (G) -- (D);
|
||||
\draw (A) -- (E) -- (B) -- (Fd);
|
||||
\draw (Cd) -- (Gd) -- (Dd) -- (Ad);
|
||||
|
||||
\draw (F) -- (A) -- (Cd);
|
||||
\draw (C) -- (E) -- (Gd);
|
||||
\draw (G) -- (B) -- (Dd);
|
||||
\draw (D) -- (Fd) -- (Ad);
|
||||
\draw (Cd) -- (E) -- (G);
|
||||
\draw (Gd) -- (B) -- (D);
|
||||
\draw (Dd) -- (Fd);
|
||||
\draw (A) -- (C);
|
||||
|
||||
\node (1u) at (barycentric cs:A=1,Cd=1,E=1) {};
|
||||
\node (2u) at (barycentric cs:Gd=1,B=1,E=1) {};
|
||||
\node (3u) at (barycentric cs:B=1,Dd=1,Fd=1) {};
|
||||
\node (4u) at (barycentric cs:F=1,A=1,C=1) {};
|
||||
\node (5u) at (barycentric cs:E=1,G=1,C=1) {};
|
||||
\node (6u) at (barycentric cs:B=1,G=1,D=1) {};
|
||||
\node (1d) at (barycentric cs:Cd=1,Gd=1,E=1) {};
|
||||
\node (2d) at (barycentric cs:Dd=1,Gd=1,B=1) {};
|
||||
\node (3d) at (barycentric cs:Dd=1,Ad=1,Fd=1) {};
|
||||
\node (4d) at (barycentric cs:A=1,E=1,C=1) {};
|
||||
\node (5d) at (barycentric cs:G=1,E=1,B=1) {};
|
||||
\node (6d) at (barycentric cs:D=1,Fd=1,B=1) {};
|
||||
|
||||
\draw[dashed] (Cd.north) -- +(0cm ,6mm );
|
||||
\draw[dashed] (Gd.north) -- +(0cm ,6mm );
|
||||
\draw[dashed] (Dd.north) -- +(0cm ,6mm );
|
||||
\draw[dashed] (Ad.north) -- +(0cm ,6mm );
|
||||
\draw[dashed] (F.south) -- +(0cm ,-6mm);
|
||||
\draw[dashed] (C.south) -- +(0cm ,-6mm);
|
||||
\draw[dashed] (G.south) -- +(0cm ,-6mm);
|
||||
\draw[dashed] (D.south) -- +(0cm ,-6mm);
|
||||
\draw[dashed] (F.west) -- +(-6mm,0cm );
|
||||
\draw[dashed] (A.west) -- +(-6mm,0cm );
|
||||
\draw[dashed] (Cd.west) -- +(-6mm,0cm );
|
||||
\draw[dashed] (Ad.east) -- +(6mm ,0cm );
|
||||
\draw[dashed] (Fd.east) -- +(6mm ,0cm );
|
||||
\draw[dashed] (D.east) -- +(6mm ,0cm );
|
||||
\end{scope}
|
||||
|
||||
\draw[hex] (1u.center) -- (1d.center) -- (2u.center)
|
||||
-- (2d.center) -- (3u.center) -- (3d.center);
|
||||
\draw[hex] (4u.center) -- (4d.center) -- (5u.center)
|
||||
-- (5d.center) -- (6u.center) -- (6d.center);
|
||||
\draw[hex] (1u.center) -- (4d.center);
|
||||
\draw[hex] (2u.center) -- (5d.center);
|
||||
\draw[hex] (3u.center) -- (6d.center);
|
||||
\draw[hex,dashed] (1d.center) -- +(0, 1.5cm);
|
||||
\draw[hex,dashed] (2d.center) -- +(0, 1.5cm);
|
||||
\draw[hex,dashed] (3d.center) -- +(0, 1.5cm);
|
||||
\draw[hex,dashed] (4u.center) -- +(0,-1.5cm);
|
||||
\draw[hex,dashed] (5u.center) -- +(0,-1.5cm);
|
||||
\draw[hex,dashed] (6u.center) -- +(0,-1.5cm);
|
||||
|
||||
\draw[hex,dashed] (1u.center) -- +(150:1.0cm);
|
||||
\draw[hex,dashed] (4u.center) -- +(150:1.0cm);
|
||||
\draw[hex,dashed] (3d.center) -- +(-30:1.0cm);
|
||||
\draw[hex,dashed] (6d.center) -- +(-30:1.0cm);
|
||||
\end{tikzpicture}
|
||||
\label{fig:dual}}
|
||||
|
||||
\caption{Triangulation d'accords et dual se rapportant à un graphe de Cayley}
|
||||
\label{fig:cayley-use}
|
||||
\end{figure}
|
||||
|
||||
\section{Formalisation}
|
||||
|
|
@ -600,14 +690,21 @@ G~:
|
|||
\item un arc étiqueté $e$ setrouve entre les sommets $U$ et $V$ si $U + e = V$.
|
||||
\end{itemize}
|
||||
|
||||
Un tonnetz peut être vu comme le graphe de Cayley du groupe cyclique
|
||||
$\mathbb{Z}_{12}$ des 12 demi-tons de la gamme occidentale muni de l'addition
|
||||
comme loi commutative et d'une partie génératrice $S$ ; pour garder l'analogie
|
||||
dans la figure \ref{fig:cayley}, nous utilisons deux générateurs libres : la
|
||||
tierce Majeur et la quinte juste. Le sommet à l'origine du graphe de Cayley est
|
||||
l'élément \emph{neutre} du groupe.
|
||||
Un tonnetz peut être vu comme le graphe de Cayley de la présentation finie
|
||||
d'un groupe, en l'occurence du groupe cyclique $\mathbb{Z}_{12}$ des 12
|
||||
demi-tons de la gamme occidentale, muni de l'addition comme loi commutative et
|
||||
d'une partie génératrice $S$. Pour garder l'analogie dans la figure
|
||||
\ref{fig:cayley}, nous utilisons deux générateurs : la tierce Majeure
|
||||
(\texttt{4}) et la quinte juste (\texttt{7}). Le sommet à l'origine du graphe
|
||||
de Cayley est l'élément \emph{neutre} du groupe. Dans nos exemples, nous
|
||||
utilisons la présentation finie suivante :
|
||||
\begin{quote}
|
||||
\texttt{g = < 4, 7; 3.4=0, 12.7=0 >}
|
||||
\end{quote}
|
||||
Dans le graphe de Cayley associé à cette présentation, l'espace se replie sur
|
||||
lui même après 4 « sauts » de tierce Majeure ou 12 « sauts » de quinte juste.
|
||||
|
||||
Chemins hamiltoniens dans le tonnetz \cite{albini_hamiltonian_2009}.
|
||||
%Chemins hamiltoniens dans le tonnetz \cite{albini_hamiltonian_2009}.
|
||||
|
||||
\subsection{Quelques mappings}
|
||||
Pour apporter des éléments de réponse aux questions des physiciens (§~%
|
||||
|
|
@ -630,16 +727,42 @@ Nous utilisons cette capacité de reconnaissance pour reconnaître et
|
|||
différencier différentes organisations spatiales des bulles dans une mousse en
|
||||
deux dimensions et plus tard reconnaître leur évolution.
|
||||
|
||||
\subsubsection{Organisation rythmique}
|
||||
La synthèse modale est un cas de sonification classique. Nous associons un
|
||||
résonnateur à chaque bulle de la mousse, ainsi les paramètres de la bulle
|
||||
sert à déterminer les paramètres du résonnateur. Ce dernier est modélisé très
|
||||
simplement par une fonction oscillante atténuée :
|
||||
$$ cos(a\cdot t)\cdot e^{-k\cdot t} $$
|
||||
Ce premier mapping se veut très simple afin de déterminer quelles informations
|
||||
sont très facilement accessibles à l'ouïe. L'Implémentation
|
||||
(§~\ref{sec:implementation}) a été menée en utilisant \modalys.
|
||||
|
||||
\subsubsection{Chemins rythmiques}
|
||||
À l'image d'un exemple de sonification du §~\ref{subsec:sonification}, le
|
||||
compteur Geiger, nous pouvons utiliser le rythme comme lien à l'organisation
|
||||
spatiale des bulles d'une mousse liquide en deux dimensions.
|
||||
|
||||
\begin{figure}[ht]
|
||||
\centering
|
||||
\subfloat[$(\Delta)$, en rouge, traverse la mousse. Les centres des bulles
|
||||
proches sont sélectionnés]{
|
||||
\includegraphics[width=.45\textwidth]{img/chemin-rythm1}
|
||||
\label{fig:rythm1}}
|
||||
\qquad
|
||||
\subfloat[Projection orthogonale des centres de bulles sur $(\Delta)$ pour
|
||||
obtenir une phrase rythmique]{
|
||||
\includegraphics[width=.45\textwidth]{img/chemin-rythm2}
|
||||
\label{fig:rythm2}}
|
||||
\caption{Extraction d'une phrase rythmique dans une mousse en deux
|
||||
dimensions}
|
||||
\end{figure}
|
||||
|
||||
On parcours par balayage le long d'une segment de droite $(\Delta)$ l'image
|
||||
d'une mousse en sélectionnant tous les centre de bulle étant à une distance $d$
|
||||
de la droite. Ces échantillons récoltés sont ensuites projetés orthogonalement
|
||||
sur $(\Delta)$. On sonifie ensuite la distance entre chaque point projeté pour
|
||||
obtenir un motif rythmique.
|
||||
obtenir un motif rythmique : nous avons ainsi une information en une dimension
|
||||
en traversant un échantillon et nous pouvons détecter une symétrie axiale d'axe
|
||||
orthogonal à $(\Delta)$.
|
||||
|
||||
Cette technique est mise en pratique par S. Adhitya dans \textsc{Sum}
|
||||
\cite{adhitya_audio-assisted_2011}, un outil permettant de sonifier
|
||||
|
|
@ -663,7 +786,7 @@ voisins, en prenant les directions \texttt{a}, \texttt{b}, \texttt{a+b},
|
|||
\texttt{-a}, \texttt{-b} et \texttt{-(a+b)}. Plongé dans un tonnetz, ceci
|
||||
correspond à une suite de notes.
|
||||
|
||||
\subsubsection{Chemins sonores augmentés}
|
||||
\subsubsection{Chemins augmentés}
|
||||
Nous avons rajouté des extensions au dessus des chemins sonores tels que
|
||||
décrits dans la section précédente : accords, mélodies plus complexes et
|
||||
rythme.
|
||||
|
|
@ -675,6 +798,7 @@ différences de distance entre le parcours dans un espace \emph{régulier} et
|
|||
déformé.
|
||||
|
||||
\section{Implementation}
|
||||
\label{sec:implementation}
|
||||
Tous les mappings ont été implémentés grâce aux outils présents à
|
||||
l'\ircam, notamment \modalys, pour la synthèse modale, et
|
||||
\openmusic\ comme environnement de programmation principal.
|
||||
|
|
|
|||
BIN
img/chemin-rythm1.png
Normal file
BIN
img/chemin-rythm1.png
Normal file
Binary file not shown.
|
After 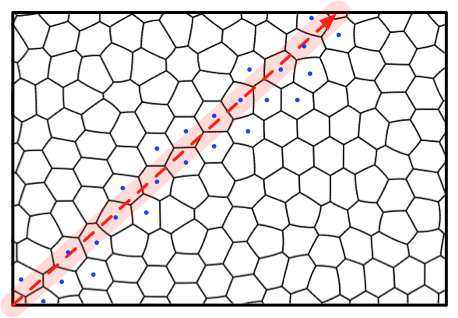
(image error) Size: 102 KiB |
BIN
img/chemin-rythm2.png
Normal file
BIN
img/chemin-rythm2.png
Normal file
Binary file not shown.
|
After 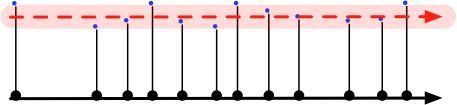
(image error) Size: 12 KiB |
Loading…
Add table
Add a link
Reference in a new issue